Further Clarification of Non-Equilibrium and Equilibrium Flashing Flows Through Top Located Safety Relief Valves (SRVs)

Non-Equilibrium Flashing Flow

            If all liquid exist at the stagnation condition (no vapor), extensive data suggest that a simple length criterion of the order of 100 mm characterizes the residence time (~ of the order of 1 ms) requirement for approaching equilibrium flashing flows which are well described by the Equilibrium Rate Model (ERM) (Fauske, 1985)

                                                                                                                                                                                                                                                                                     (1)

where is the latent heat of evaporation, v_fg is the change in liquid-vapor specific volume, T is the temperature and C is the liquid specific heat, all evaluated at stagnation condition.  In contrast, the maximum non-equilibrium mass flux as the length approaches zero is given by

                                                                                                                                                                                                                                                                          (2)

where P is the stagnation gauge pressure and ρ is the liquid stagnation density.  Considering that

                                                             G_max >> G_ERM                                                (3)

determines the relevant velocity and the length requirement of about 100 mm for all liquid stagnation condition (near saturated liquid and subcooling).

Equilibrium Flashing Flow

            If liquid-vapor (void fraction > 0.1) exist at the stagnation condition, the length L (mm) required to satisfy a residence time of about 1 ms is given by

                                                             L (mm) = 1 (ms) g G_ERM/r (mm/ms)                 (4)

resulting in a length requirement much smaller than 100 mm.  In other words 100 mm length requirement is only relevant to all liquid stagnation conditions.

            Given the above observations, Eq. 1 can be used without modification to estimate flashing two-phase flows through top located SRVs for relief sizing purposes using the following equation (Fauske, 1999) if Eq. 4 and stagnation vapor void fraction a > 0.1 are satisfied

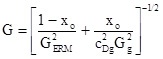                                                                                                                                  (5)

where x_o is the stagnation quality, C_Dg is the valve manufacturer certified discharge coefficient for gas flow, and G_g is the gas flow (sonic or subsonic) through an ideal nozzle.  An example of comparison with Eq. 5 and experimental data is illustrated below.  In this case Eq. 4 suggests a length L of only about 10 mm to satisfy equilibrium flashing which is clearly satisfied by the SRV.  Furthermore a stagnation quality of x_o = 0.001 is equivalent to a = 0.14 at the 10.6 bar stagnation pressure.

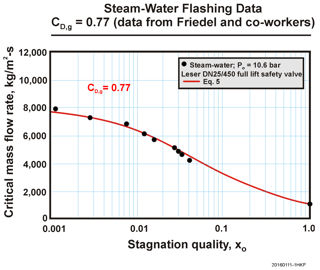            Both requirements to satisfy equilibrium flashing flow are sensitive to the stagnation pressure.  As an example consider a stagnation pressure of 62 bar, result in L = 40 mm and x_o = 0.0048, which is consistent with experimental data (Sozzi and Sutherland, 1975.)

References

Hans K. Fauske, 1985, "Flashing Flows Or: Some Practical Guidelines for Emergency Releases," Plant/Operations Progress, July, 1985.

Hans K. Fauske, 1999, "Determine Two-Phase Slows During Releases," Chemical Engineering progress, February, 1999.

Sozzi, G. L. and Sutherland, W. A., 1975, "Critical Flow of Saturated and Subcooled Water at High Pressure," Report NEDO-13418, General Electric Company, San Jose, CA (July).

For more information regarding this or other relief system design concerns, contact us at info@fauske.com, 630-323-8750