Peak Pool Boiling Critical Heat Flux True Hydrodynamic Limitation

By Hans K. Fauske, D.Sc., Emeritus President, ANS Fellow, AIChE Fellow, NAE Member

As often claimed, the classic hydrodynamic instability theory by Zuber (1958) does not provide the upper external hydrodynamic limitation to onset of the heat transfer crisis for well-wetted horizontal surface,

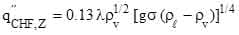     (1)

where 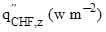= pool boiling critical heat flux,  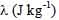= latent heat of evaporation, ρ_v (kg m^-3) = vapor density, g (9.8 m s^-2) = gravitational constant, (kg s^-2) = liquid surface tension, and ρ_l (kg m^-3) = liquid density. Here, I propose that the upper limiting value of the heat flux (independent of surface conditions such as porous, polished, or nanoscopically smooth surfaces) is determined by the onset of fluidization, i.e., change in flow regime from liquid to vapor continuous condition.

The superficial vapor velocity j_v corresponding to fluidization can be estimated from (Wallis, 1969), 

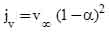     (2)

where α is the volume fraction of liquid droplets, and 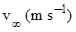 is the terminal droplet velocity given by (Levich, 1962),

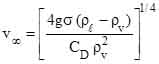     (3)

Combining Eqs. (2) and (3) and setting C_D = 1 and α = 0.6 (corresponding to a state when spherical liquid droplets no longer are touching each other) results in the minimum fluidization velocity,

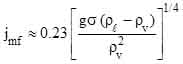     (4)

and the peak critical heat flux 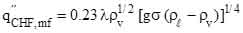     (5)

It follows that 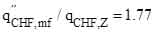 . Here we note that the highest measured deviations from Zuber’s instability theory is a factor of 1.78 obtained on microporous surfaces with the highly-wetting FC-72 fluid (Rainey et al., 2003).

In summary, considering an appropriate hydrodynamic limit based upon a flow regime change from liquid to vapor continuous condition due to incipient fluidization (Eq. 5), this limit is clearly substantiated based upon the highest reported heat flux values obtained with well-wetting surfaces at different pressures. As such, the microporous surfaces used by Rainey et al., provide the maximum possible heat removal rates.

References

Levich, V. G., 1962, “Physiochemical Hydrodynamics,” Prentice Hall .

Rainey, K. N., et al., 2003, “Pool Boiling Heat Transfer Microporous Surfaces in Surfaces in FL-72,” Journal of Heat

Transfer, Vol. 125/75 (February).

Wall is, G. B., 1969, “One-Dimensional Two-Phase Flow,” McGraw-Hill .

Zuber, N., 1958, “On the Stability of Boiling Heat Transfer,” ASME J. Heat Transfer 80(2), pp . 711-720.