1. Introduction
Hydrogen explosions with severe damages during nuclear severe accidents are not hypothetical events. Hydrogen explosion risk is real. In the world of Probability Safety Assessment (PSA), determination of hydrogen explosion risk has been a major areas of interest since the explosion of hydrogen in the containment of Three Mile Island unit 2 (TMI-2) in March, 1979 [5]. The most recent evidences are the explosions in the reactor building of unit 1 and unit 3 of Fukushima Daiichi reactors [6]. Interestingly, the hydrogen explosion in unit 3 reactor building was very different from the explosion in unit 1. The explosion in unit 1 was directed horizontally from the top floor of the reactor building. Building roof and sidings were blown away by the explosion but concrete pillars remain intact with little damage. The explosions in unit 3 were quite different and highly energetic. There appeared to be (from video recordings) at least two explosions. The first one was less energetic and directed horizontally (similar to that of unit 1). The second one was directed vertically with an almost perfect spherical fireball appearing above the building and shooting up very high into the sky. Large chunks of materials appeared to be carried up high with the fireball. Contrary to unit 1, the concrete pillars on the building top floor as seen from pictures were highly damaged.
In this article, a new methodology is presented to quantitatively calculate the likelihood of hydrogen explosions in the form of DDT (Deflagration to Detonation Transition) during a severe accident [1]. Determination of the probability of the DDT during severe accident scenarios thus far has been subjected to qualitative expert opinions. The method of Sherman and Berman [2], which gives the probability of DDT, requires qualitative engineering judgment that could be very subjective. There have been no proposed quantitative methods to calculate such probabilities to the best of the author’s knowledge. The proposed method enables us to quantify a probability of DDT for any given severe accident sequence that can be simulated by a severe accident analysis code. Different accident sequences will have different characteristics of cladding oxidation, hydrogen production rate and hydrogen release rate, and, therefore, will have different probabilities of DDT. The proposed definition of DDT probability is based on the physics of combustion and an assumption that random ignition is always present at any time as experienced in the TMI-2 and Fukushima Daiichi accidents. MAAP analyses are used to simulate accident sequences and to calculate the 7λ criteria. The purpose of MAAP analyses is to determine the containment atmospheric conditions whether flammable or detonable conditions exist during the course of an accident. The concentrations of flammable gases depend largely on the balance between the generation and the consumption of combustible gases during individual accident scenarios. The 7λ criterion is the latest method proposed by an expert group commissioned by OECD/NEA that set the standard for DDT evaluation at present time [3]. DDT conditions can be calculated at every time step of the accident simulation in every containment node. Here the DDT condition refers to the gaseous mixture that has compositions that meet the criteria of flame acceleration (FA) and the detonation cell size that allows DDT to develop within the characteristic length of the compartment. When the DDT condition is detected in the accident simulation, it means that all necessary conditions for DDT are present.
2. Proposed Definition of DDT Probability
The proposed definition of DDT probability is based on the physics of combustion that can be modeled in a severe accident code and an assumption that random ignition is always present with equal chance at any time. The probability that DDT occurs is simply assigned as 1 if only detonable conditions exist, i.e. there is a DDT time window that is long enough such that there is no question whether a random ignition is present or not. As shown in Figure 1, if a downwardly flammable non-DDT condition precedes the DDT window, the DDT probability is simply defined as a ratio of the DDT time window to the combined time of DDT window and the downwardly flammable non-DDT window (Figure 2). The downwardly flammable non-DDT conditions that precede the DDT window have a potential to consume the available combustible gases at that time and prevent DDT from occurring afterward. Hence, the preceding flammable non-DDT conditions reduce the probability of DDT during the DDT window.
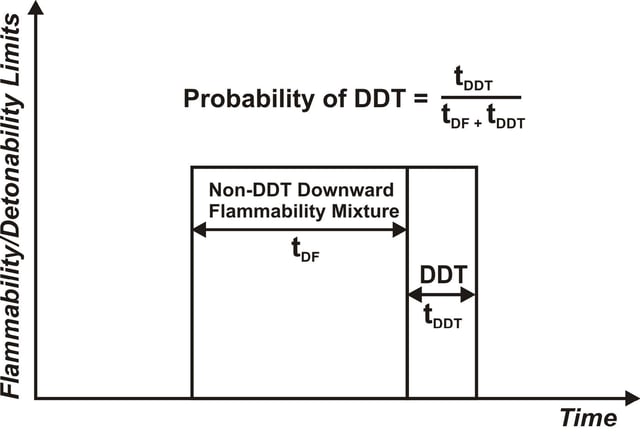 Figure 1. Proposed Definition of DDT Probability
Figure 1. Proposed Definition of DDT Probability
When DDT occurs, it shall be assumed that the containment will fail catastrophically. Hence, the DDT probability is also the probability of failing containment by DDT. That is, the DDT probability in any building node denoted by “i” according to our proposed definition is given by
tDDT, i
PDDT, i = —————
tDDT, i +tDF, i
Where tDDT, i = DDT time window for node i during which continuous detonable conditions exist
tDF, i = Deflagration time window for node i during which continuous downwardly flammable conditions in node i exist before the onset of the DDT window
The DDT probability is calculated based on the time ratio of detonable mixture conditions. There is no knowledge about ignition sources that can ignite these mixtures. However, it is simply assumed that there is equal likelihood of random ignition over the flammable or detonable periods for the purpose of expressing the probability. Since DDT conditions can occur globally or locally the definition given above may be applied to either global or local conditions of the containment. However, it is more likely that DDT occurs locally due to local release and accumulation of hydrogen.
3. Severe Accident Code Simulation of Hydrogen Generation, Distribution and Consumption
The proposed approach for the DDT probability requires information of local and global gaseous compositions, pressures and temperatures of the reactor containment during a severe accident. This information can be provided by a simulation of a severe accident scenario of interest with a severe accident code such as MAAP [4]. The information will be used for determination of downwardly flammable time window and DDT time window.
The purpose of severe accident analysis is to determine the containment atmospheric conditions and whether flammable or detonable conditions exist during the course of an accident. The concentrations of flammable gases depend largely on the balance between the generation, the consumption and transport of combustible gases during individual accident scenarios. The MAAP code simulates the core melt process and generates the hydrogen source terms to the containment. The distribution of hydrogen in the containment will depend on the details and how the containment is partitioned into sub-compartments in the input. The simulation should be as realistic as possible with regard to mechanisms that consume combustible gases. Detailed explanation of models and assumptions that are made to reflect the physics of the combustion phenomena in the accident simulation can be found in [1].
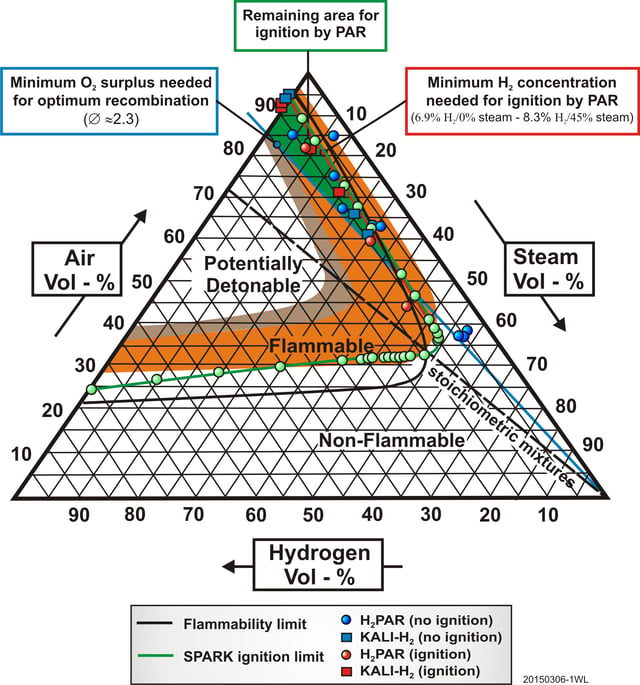
Figure 2: Flammability Limits [7] and PAR-induced Ignition Limits [8]
4. DDT Evaluation Methods
Two methods for DDT evaluation have been proposed. The older method of Sherman and Berman [2] which assigns the probability of DDT in five categories, i.e., DDT is highly likely (p=0.99), DDT is likely (p=0.9), DDT may occur (p=0.5), DDT is possible but unlikely (p=0.1) and DDT is highly unlikely to impossible (p=0.01). This method classifies the combustible gaseous mixture into five mixture classes based on detonation cell widths. The method also classifies the compartment that contains the combustible mixture into five geometric classes according to the degree to which the geometry of the compartment and obstacles inside it promote flame acceleration. Large but confined geometries with obstacles in the path of the expanding unburned gases are considered most favorable for flame acceleration. If transverse venting is added to the above path, it is considered a feature that hinders flame acceleration. If obstacles are removed from the path, the geometry is considered neutral to DDT. Large volumes with hardly any obstacles and large amount of venting transverse to the flame path are classified as unfavorable to flame acceleration. Last but not least, a totally unconfined geometry at large scale is classified as so unfavorable to flame acceleration. Based on which mixture class and which geometric class are assigned to the conditions of interest, one of the five DDT probability categories is assigned. The problem and the difficulty with this method lie in the determination of geometric class which requires too much qualitative engineering judgment. Actual plant geometries can be very complicated such that subjective judgment by different people can lead to diverse answers.
The more recent method proposed by an expert group commissioned by OECD/NEA. The group issued the so-called “State-of-the-Art Report (SOAR) on Flame Acceleration and Deflagration-to-Detonation Transition in Nuclear Safety” that set the standard for DDT evaluation at the present time [3]. The SOAR approach is based on theoretical consideration and experimental data on flame acceleration (FA) and deflagration to detonation transition (DDT) up to the year 1999 with most experiments performed from 1993 to 1999. It is important to realize that the detonation cell width approach based on literature up to the 1980s is not the same as the SOAR approach. The SOAR approach uses a σ-criterion for flame acceleration and a 7λ criterion for DDT as pre-requisite conditions. The σ-criterion is a measure of mixture reactivity to promote flame acceleration. σ refers to an expansion ratio defined as unburned-to-burned mixture density ratio. The expansion ratio must be greater than the critical expansion ratio (σcritical) for flame acceleration (which is a prerequisite to DDT) to occur. While the expansion ratio represents the reactivity of the mixture, the critical expansion ratio is regarded as a boundary between slow flames and fast accelerated flames. The critical expansion ratio is a function of temperature. The critical expansion ratio decreases with increasing temperatures. The detonation cell width (λ) is a basic parameter used for characterizing the sensitivity of a mixture to detonation initiation. The 7λ criterion is a measure of the effect of scale on the detonation onset. Experimental data performed extensively in the 1990s to support the SOAR report generally showed a good agreement with the 7λ criterion over a wide range of scales and mixture compositions. Both criteria are as necessary conditions for onset of DDT. Meeting or exceeding these criteria does not necessarily result in DDT. The criteria are only necessary conditions. The criteria are not sufficient conditions for DDT. Using this methodology for quantifying DDT likelihood is the same as assuming that these criteria are sufficient conditions for the onset of DDT.
5. Example
As examples, the proposed definition is applied to severe accidents in a typical 1000 MWe PWR with a large dry containment. The first example assumes failure of core cooling during a hot shutdown that leads to core melt, vessel failure, and MCCI. A large amount of hydrogen gas was produced but the containment atmosphere was inert by steam. Late into the accident, long after vessel failure, containment spray actuation was assumed to reduce containment pressure by condensation of steam, and the cavity was eventually flooded by spray water. Figure 3 shows gaseous volume fractions of steam, H2, CO, and O2 as a function of time for the case when the cavity is flooded by spray water. Figure 4 shows gaseous volume fractions of steam, H2, CO, and O2 for another case when the cavity flow path does not allow cavity flooding by spray water. The DDT probabilities calculated and monitored for more than 3 days for each case are also shown in both figures. For the flooded cavity case, the DDT probability changes from zero to non-zero values when H2 volume fraction increases to 14% while steam volume fraction (which is high initially) decreases to 15%. The DDT probability increases to a value of 0.75 after 3 days into an accident as an ultimate result of a large amount of combustible gases (mostly hydrogen) generated from MCCI in a basaltic concrete.
However, for the case when the cavity is assumed not to be flooded by spray water and to remain dry under MCCI conditions, the molten debris pool remains very hot inside the cavity. The MCCI-driven molten debris pool can generate hot “flying particles” through the gas bubbling and melt eruption process [9]. These hot particles are assumed to ignite the flammable gas mixture formed in the cavity. This process can potentially continue until a sufficient amount of oxygen has been consumed to the point of the containment-wide oxygen-starved condition. As a result, the DDT probability remains zero through the entire accident sequence (Figure 4). This example demonstrates that the concentration of combustible gases (which is produced by the MCCI process) is controlled to low levels by the high temperature nature of the MCCI process itself provided that the cavity flow paths are not too restricted to allow oxygen to be brought to the cavity from the rest of the containment. There is uncertainty in the combustion mode over the MCCI molten debris. The combustion mode assumed in this study is multiple hot-surface-induced deflagrations. However, burning as diffusion flames over the molten debris is also possible. In either mode, hydrogen would be consumed and the trend would be the same.
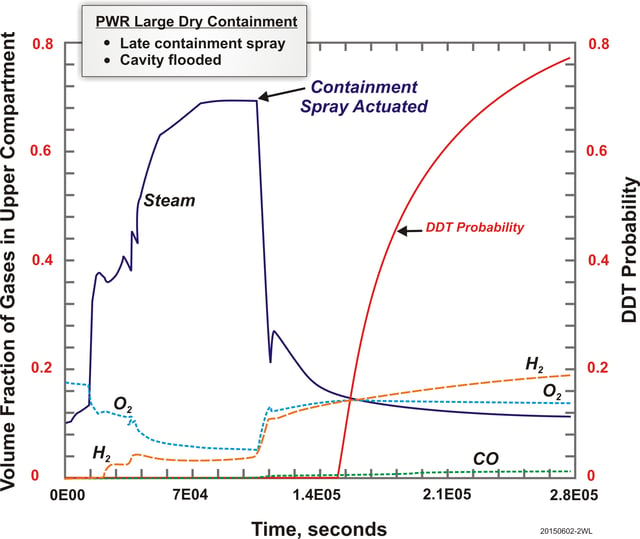
Figure 3: DDT Probability of Severe Accident Sequence in Example PWR
with Flooded Cavity due to Late Containment Spray Actuation
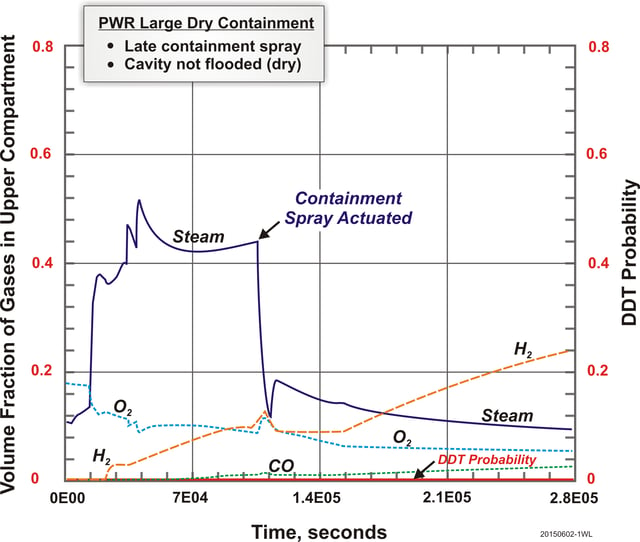
Figure 4: DDT Probability of Severe Accident Sequence in Example PWR with
Late Containment Spray actuated but Cavity Remained Dry
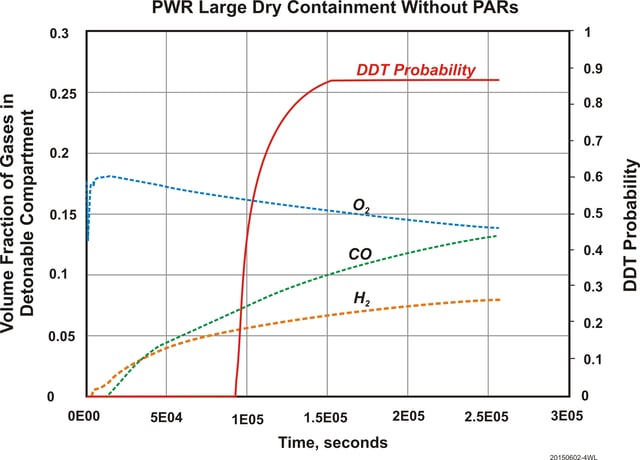
Figure 5: DDT Probability of Severe Accident Sequence in Example PWR without PARs
As another example, the proposed definition is applied to a simultaneous large LOCA and SBO accident in a larger PWR with a large dry containment. The accident leads to core melt, vessel failure and MCCI with limestone concrete in the cavity. In this case, a large amount of CO and lesser amount of H2 are generated. The DDT probability was calculated and monitored for 3 days. The DDT probability peaks at a value of 0.866 as an ultimate result of a large amount of combustible gases generated from MCCI (Figure 5). The time when the peak value of 0.886 is attained corresponds to the time when the detonation cell width has increased beyond 2 m, the size over which DDT was never observed in any experiments [3]. It is used in this study as a detonation cell width cutoff criterion. The detonation cell width decreases and increases forming a U-shape during the time when DDT probability rises from zero to the peak value. The decrease in detonation cell width is due to an increase in combustible gas concentrations, while the increase is caused by an increase in containment pressure which increases about 0.8 bar to a total pressure of 5.5 bars during the time period.
However, when the plant is assumed to be equipped with a reasonable number of PARs commensurate with severe accident considerations (such as ~ 50 kg-mole/hr of combustible gas generation rate from MCCI), the calculated DDT probability turns out to be zero (Figure 6). In this example, CO is not modeled to be oxidized to CO2 by PARs. If CO oxidation is modeled, CO concentration would be less than what is shown in Figure 6, and H2 concentration would be higher.
It is well known that the hydrogen recombination rate of PARs is too slow to cope with the extremely fast zirconium alloy-steam reaction rate (say, ~0.3 kg/s or more) during the core melt process. This second example demonstrates that PARs has a potential to control combustible gases generated from the MCCI process to the levels where DDT is not possible. The generation rate of combustible gases from the MCCI process is not too fast and can be coped with by the recombination rates of PARs.
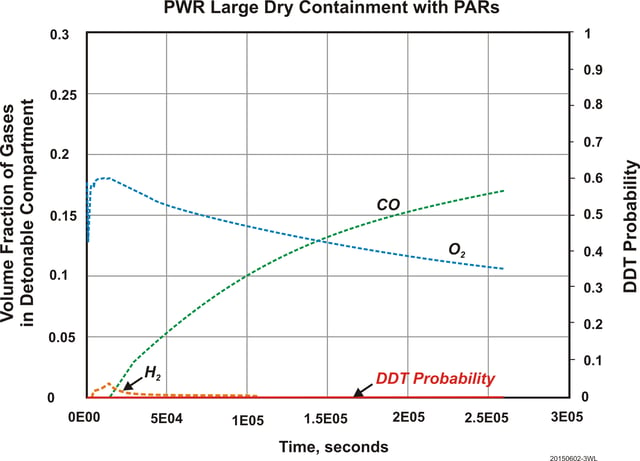
Figure 6: DDT Probability of Severe Accident Sequence in Example PWR without PARs
6. Summary- The method is quantitative and objective and is entirely based on simulation of accident scenarios using a severe accident code that calculates the accident conditions as mechanistically as possible using the 7λ method to quantitatively calculate the DDT limits.
- The method removes the subjective and qualitative judgement required in the past practice.
- The calculated probability is a function of accident time, and is a unique signature of an accident sequence.
- The DDT risk of different accident scenarios can be easily ranked.
For more information or to discuss, please contact us at info@fauske.com
